
Kyvadlo se nachází všude kolem nás, aniž si to uvìdomujeme a vnímáme ho. Pomocí kyvadla se v technice a fyzice mìøí dvì velmi dùležité velièiny èas a gravitaèní zrychlení. Snad nejdùležitìjší fyzikální velièinou, která existuje je èas.
Èas plyne od poèátku dìjin a k jeho mìøení se používalo vždy slunce. Sluneèní hodiny jsou k vidìní na mnoha domech, jejich velkou nevýhodou je, že pracují jen pokud svítí slunce. Sluneèní hodiny byly znaènì nepøesné a záviselo na místì kde se hodiny nacházely. Kyvadlo se zaèalo používat v dobì Keplera, Galilea, Newtona, Huygense.
Huygense do vývoje kyvadlových hodin pøispìl nejvíce. Huygens se narodil v roce 1629 v Haagu a zemøel v roce 1695 po dlouhé nemoci v Haagu. V letech 1645 ÷ 1647 studoval práva a matematiku na Leydonské univerzitì. Ve studiu pokraèoval na kolegiu Arausiacum v Bredì do roku 1649. Do roku 1666 žil se svým otcem v Haagu a dopracoval se k nìkolika objevùm : teorii pravdìpodobnosti, zákonu elastického otøesu, zákonu odstøedivé síly, geometrické optiky kyvadlových hodin, Saturnových prstencù a satelitu Titan. V roce 1666 pøijal Huygens pozvání mìsta Paøíže jako èlena novì založené vìdecké akademie. V roce 1673 zde publikoval své nejvýznamnìjší dílo „Horologium oscillatorium sive motu pendolorum ad horologia aptato", kde shrnul teoretické vlastnosti kyvadla a objev svých kyvadlových hodin. V roce 1681 se vrátil do Haagu, kde žil až do své smrti. Nìkolikrát navštívil Londýn a pøi jeho poslední návštìvì roku 1689 se èasto potkával s Newtonem. Huygens své kyvadlové hodiny zkonstruoval bez znalosti Galileovy myšlenky o regulaci hodin pomocí kyvadla.
Fyzické kyvadlo, používané v kyvadlových hodinách, je sestrojeno ze závìsu, èoèky, tyèe.

Obr.1.1 náčrt kyvadla v hodinách
Jako první se používal závìs pomocí vláknové smyèky, který vynalezl Huygens. U pøesných kyvadel se používán konstrukce Galilea zavìšení na bøitech, pozdìji se používá pérový závìs, který zkonstruoval Clement roku 1676.
Nejlepší a také na výrobu nejobtížnìjší je bøitový závìs, kde je osa kyvadla naprosto pevnì uložena a kyvadlo se kývá v jedné rovinì a rušivé úèinky jako lidská a seismická èinnost, rotace Zemì jsou ménì rušivé.
Pérový závìs se v pøesných kyvadlových hodinách zaèal používat asi v druhé polovinì 19. století. Pøesný pérový závìs není tak obtížné vyrobit jako bøitoví a pro namáhání na tah jej lze zhotovit v malém rozmìru
. Pro stálost kyvù kyvadla se používá závaží na konci kyvadla zvaná èoèka, pro svùj tvar jak lze vidìt na starých kyvadlových hodinách.
Pøesný chod kyvadlových hodin nejvíce ovlivòuje tyè kyvadla, vlivem teploty se mìní její délka a tím pádem umístìní tìžištì a èehož vyplývá zmìna doby kyvu kyvadla. Graham ( 1675 - 1751) proto použil jako první tyèí døevìných místo kovových pro jejich nízkou tepelnou roztažnost. Dále byli pokusy s tyèemi z bøidlice a ze skla. Roku 1726 vynalezl Harrison roštové kyvadlo, kde èoèka byla zavìšena na systému tyèí ze dvou kovù s vhodnì se rùznícími koeficienty tepelné roztažnosti tak, aby se jejich vzájemná tepelná roztažnost kompenzovala. Naproti tomu Jürgensen naopak mìnil polohu tìžištì pomocí posouvajícího se závažíèka, nazvaného dle Huygense „bìžcem Huygensovým". Pozdìji byl vynalezen talíø, na který se kladou závažíèka. Roku 1727 sestrojil Graham rtuťové kyvadlo, což byla ocelová trubice naplnìná rtutí do urèité výšky, jako náhrada èoèky. Toto kyvadlo bylo zdokonaleno a propracováno roku 1891 Z. Rieflerem. Poslední pøekotné období vývoje kyvadlových hodin nastalo roku 1891, kdy Guillaume zhotovil invarové kyvadlo. Tyè byla zhotovena z materiálu s nepatrnou tepelnou roztažností oproti materiálu èoèky. Èoèka byla opøena o stavìcí matku a roztahovala se pouze horním smìrem, tím se vykompenzovala nepatrná tepelná roztažnost tyèe. Roku 1910 se podaøilo vyrobit tyè z taveného køemene. Toto kyvadlo mìlo výborné výsledky, ale bylo velmi drahé a snadno se rozbilo, kvùli køehkosti køemene.
Nejúèinnìjším opatøením používajícím se od druhé poloviny 18. století, je uzavøení hodin do vzduchotìsného uzávìru. Vyøešil se tím problém vlivu hustoty mìnící se tlakem vzduchu. Pøed zavedením kyvadla do èasomíry byla nepøesnost pøi stanovení èasu okolo 1 minuty, po zavedení kyvadlo okolo roku 1700 je stanovena nepøesnost na 1 ÷ 2 sekundy. Kolem roku 1800 už je nepøesnost na 1 sekundì. V období 1800 ÷ 1850 nastává pokrok v konstrukcích kyvadla a pøesnost je už 0,1 sekundy a pozvolna se zvìtšuje. Na zaèátku 20. století je pøesnost hodin na 0,02 sekundy, ale pøesnost kyvadlových èasomìrù je podstatnì lepší. Vynálezem fotografického zenitteleskopu lze docílit za pøíznivých sluneèních podmínek pøesnosti 0,002 sekundy, která se rovná výkonu mimoøádnì pøesných kyvadlových èasomìrù. Po tomto období ustupuje kyvadlo do pozadí jako prvoøadý normál èasový a èasomìrný. Další vývoj pøesných èasomìrù spoèívá na zcela jiných fyzikálních principech, umožòujících vìtší pøesnosti, nepostradatelné pro nìkteré obory moderních vìd.
Pøíklady kyvadel pro hodiny :

Obr 1.2 Roštové kyvadlo s neměnitelnou kompenzací dle Harrisona

Obr 1.3 Roštové kyvadlo s měnitelnou kompenzací podle Kesselse

Obr 1.4 Hardyho rourové kyvadlo
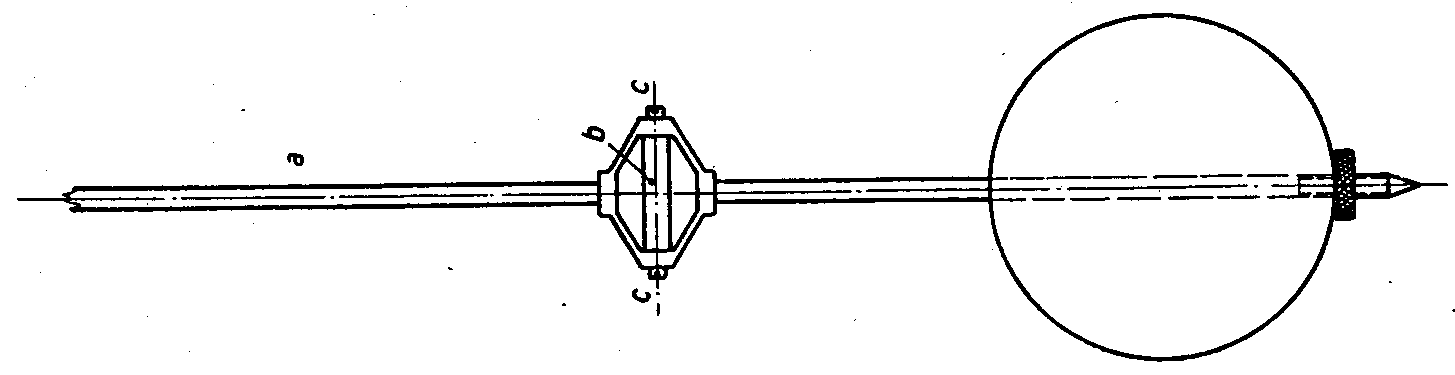
Obr 1.5 Stampferovo kyvadlo
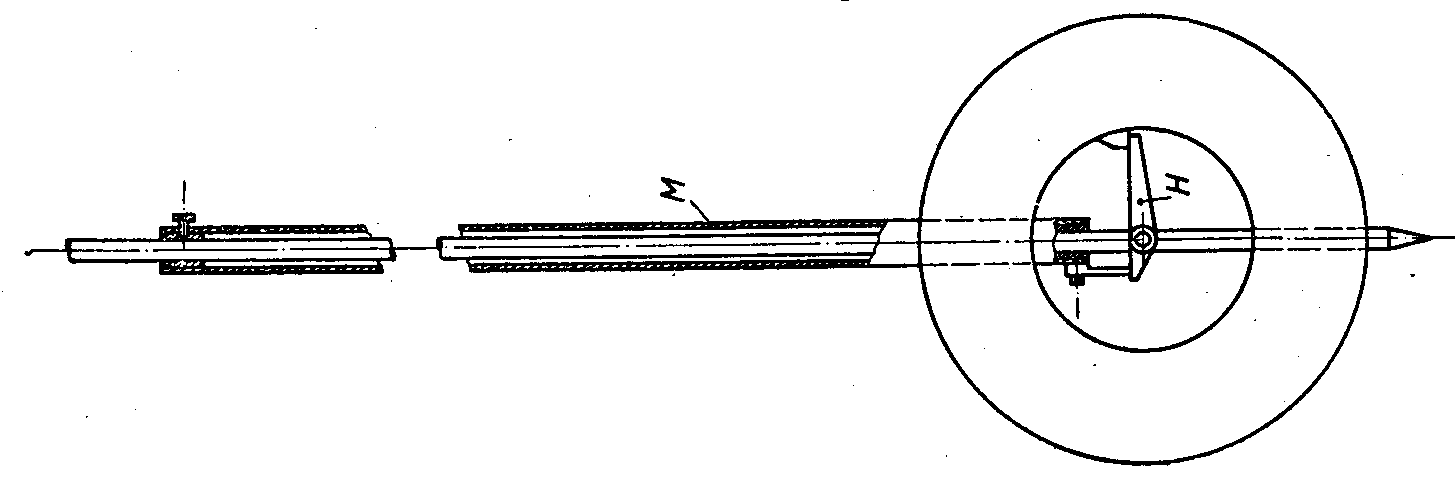
Obr 1.6 Kyvadlo podle Ellicota a Deparcieuxe
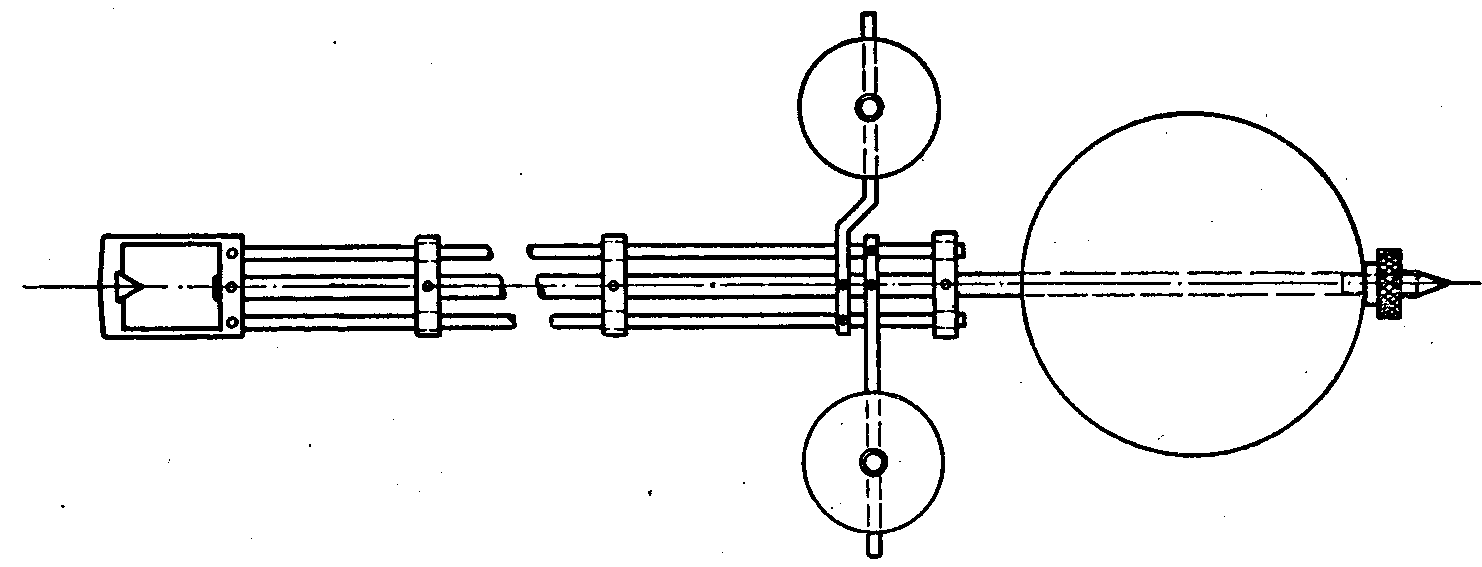
Obr 1.7 Mahlerovo kyvadlo
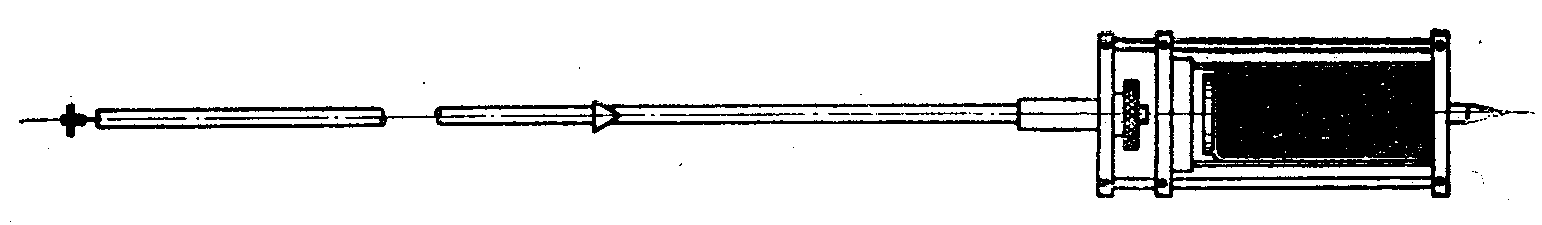
Obr 1.8 Rtuťové kyvadlo Grahamovo
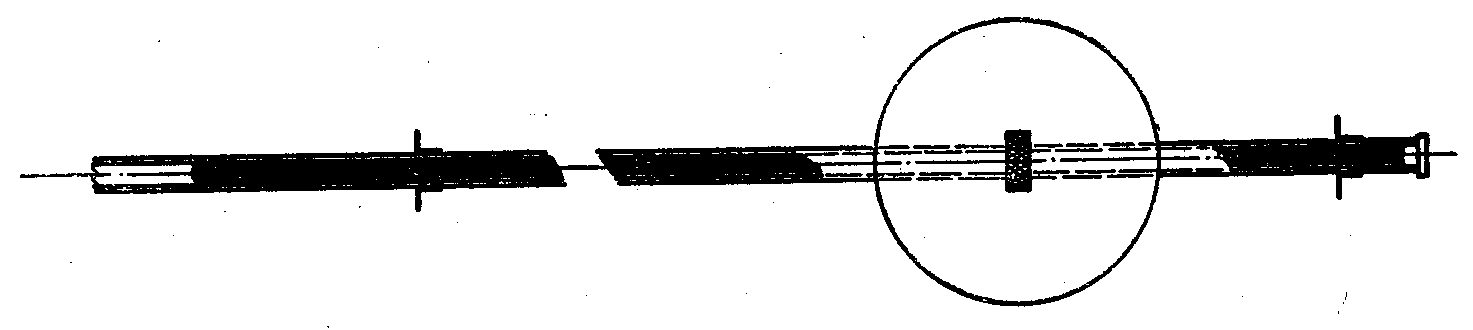
Obr 1.9 Rtuťové kyvadlo podle Rieflera
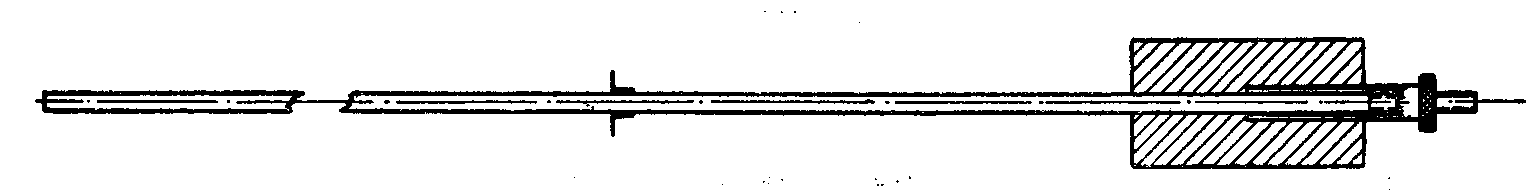
Obr 1.10 Invarové kompenzační kyvadlo
Další velmi dùležitou fyzikální velièinou,
se kterou se každý z nás setkává, je gravitaèní
zrychlení. Zvykli jsme si používat je jako konstantu, to
ale není pravda a gravitaèní zrychlení se mìní
jak s místem na Zemi, tak s èasem, protože závisí
i na vzdálenosti Mìsíce od Zemì. Gravitaèní
zrychlení se mìøí jednak absolutní a
jednak relativní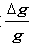 vùèi jedné stanovené stanici. K mìøení
se používají dva typy kyvadla. Prvním typem je matematické
kyvadlo, kde hmota je uložena na konci tyèe a druhý konec
tyèe pevnì uložen a platí pro nì
vùèi jedné stanovené stanici. K mìøení
se používají dva typy kyvadla. Prvním typem je matematické
kyvadlo, kde hmota je uložena na konci tyèe a druhý konec
tyèe pevnì uložen a platí pro nì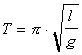 . Druhý typ používá nehmotnou tyè a kyvadlo
je zkonstruováno jako reverzní kyvadlo, poprvé bylo
použito v letech 1817 ÷ 1818 M.Karterem.
. Druhý typ používá nehmotnou tyè a kyvadlo
je zkonstruováno jako reverzní kyvadlo, poprvé bylo
použito v letech 1817 ÷ 1818 M.Karterem.
Teorii o gravitaèním poli zemì popsal Isaac Newton v díle „Philosophia naturalis principia mathematica" (Londýn 1687), kde uveøejnil také gravitaèní zákon a pohybové zákony. Již v této teorii zformuloval myšlenku rozdìlení gravitaèního pole Zemì po povrchu.
Pokud víme, že gravitaèní pole Zemì je rozdìleno po jejím povrchu, musíme si položit otázku „Jaký tvar má Zemì ?". Již staøí øekové vìdìli, že Zemì má tvar sferoidu. Zjistili to z experimentálního mìøení úhlù mezi pøímkami mìsto - obzor, Slunce - mìsto. Jedním z experimentátorù byl Erotosthenes, který mìøil v Alexandrii a v Syene v Egyptì. Vzdálenost mezi tìmito mìsty urèil z délky pochodu karavany velbloudù. Poté se dlouhou dobu vìøilo, že Zemì je placka. Tuto teorii popøel Magellan obeplutím Zemì, z toho lidé usoudili, že Zemì je koule. Teprve v letech 1684 ÷ 1718 Giovanni - Domenoco zjistil tvar Zemì pomocí zmìøení délky oblouku severnì a jižnì od Paøíže. Bohužel, jak se ukázalo chybnì, neboť tvrdil, že Zemì je rotaèní sferoid. V roce 1672 Richer provedl mìøení délky periody kyvadla v Caynu v Jižní Americe a v Paøíži. Zjistil, že jeho kyvadlové hodiny se oproti Paøíži opožïují o 2 minuty a 28 sekund za den. Postavil matematické kyvadlo a mìøil jeho dobu periody kyvu každý týden po dobu 10 mìsícù a tím si potvrdil své zjištìní. Tohoto mìøení využil Newton a zformuloval teorii v díle Principia a urèil tvar Zemì na zploštìlí sferoid, kde pomìr os Zemì je v pomìru 230 : 229. Tuto teorii potvrdil z mìøení Nichers. Nicménì mezi Newtonovou teorii a Giovanni - Domenicovou teorii vznikl ostrý spor, neboť Giovanni - Domenico se své teorie nechtìl vzdát. Teprve roku 1735 je Newtonova teorie potvrzena definitivnì.
Významným experimentátorem s teoretickým
kyvadlem byl Bouquer. Ten v roce 1737 objevil závislost délky
tyèe kyvadla na teplotì a doby periody na odporu vzduchu.
Urèil vztah 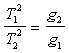 , kde T1, T2 jsou doby kyvu v rùzných místech a g1,
g2 jsou gravitaèní zrychlení v rùzných
místech. Pomocí tohoto vztahu lze zjistit gravitaèní
zrychlení pouze z pomìru kvadrátu doby kyvu a jednoho
známého gravitaèního zrychlení. Další
pokusy provádìli Picard a LaGondamine. Pokusy kulminovali
prací Borda a Cassiniho v roce 1792 na observatoøi v Paøíži.
Dalším pokraèovatelem zjišťování gravitace
na povrchu Zemì byl Bessel, který urèil gravitaci
v Berlínì. Systematicky mapovat povrch Zemì zaèal
až Henry Karter, v roce 1817 postavil fyzické kyvadlo s promìnnou
délkou tyèe pro mìøení gravitaèního
zrychlení. Vletech 1820 ÷ 1825 postavil kyvadla od Londýna
k západní Indii a odtud až k Spitzberkám. Pomocí
jeho kyvadla byla mapována celá Zemì. Jedním
z mnoha badatelù byl Lütke z Ruska, který zkoumal gravitaèní
zrychlení po celé Zemi v období 1826 ÷ 1829.
Dalšími badateli byli De Freyument z Francie, Duperry 1822 ÷1825,
Francis Baily 1827 ÷ 1840, který experimentoval s více
než 40 odlišnými kyvadly a urèoval jejich charakteristické
vlastnosti. Charles Wilkes z USA 1838 ÷ 1842.
, kde T1, T2 jsou doby kyvu v rùzných místech a g1,
g2 jsou gravitaèní zrychlení v rùzných
místech. Pomocí tohoto vztahu lze zjistit gravitaèní
zrychlení pouze z pomìru kvadrátu doby kyvu a jednoho
známého gravitaèního zrychlení. Další
pokusy provádìli Picard a LaGondamine. Pokusy kulminovali
prací Borda a Cassiniho v roce 1792 na observatoøi v Paøíži.
Dalším pokraèovatelem zjišťování gravitace
na povrchu Zemì byl Bessel, který urèil gravitaci
v Berlínì. Systematicky mapovat povrch Zemì zaèal
až Henry Karter, v roce 1817 postavil fyzické kyvadlo s promìnnou
délkou tyèe pro mìøení gravitaèního
zrychlení. Vletech 1820 ÷ 1825 postavil kyvadla od Londýna
k západní Indii a odtud až k Spitzberkám. Pomocí
jeho kyvadla byla mapována celá Zemì. Jedním
z mnoha badatelù byl Lütke z Ruska, který zkoumal gravitaèní
zrychlení po celé Zemi v období 1826 ÷ 1829.
Dalšími badateli byli De Freyument z Francie, Duperry 1822 ÷1825,
Francis Baily 1827 ÷ 1840, který experimentoval s více
než 40 odlišnými kyvadly a urèoval jejich charakteristické
vlastnosti. Charles Wilkes z USA 1838 ÷ 1842.
Významným experimentátorem byl Bessel, který mìøil gravitaèní zrychlení pomocí matematického kyvadla v letech 1825 ÷ 1827 a v roce 1835 v Königsbergu a Berlínì. Vypracoval teorii symetrického fyzického kyvadla s vymìnitelnými nožovýmí bøity místo èoèek.. Bessel dokázal, že pokud nožové bøity jsou cylindrické, jejich efekt lze kompenzovat reverzním kyvadlem. Pokud nejsou stejnì cylindrické jejich rozdíl lze odstranit jejich vymìnitelností. Podle Besselovy teorie postavila firma A.Repsold & Syn z Hamburku kyvadlo, které se používalo na observatoøi v Ženevì. Toto kyvadlo se použilo pro zmìøení gravitaèního zrychlení ve Švýcarsku v letech 1866 ÷ 1872.
Obr. 1.11 Repsold - Besselův reverní kyvadlový přístroj
Roku 1864 zaèal mìøit gravitaèní zrychlení profesor Sawitsch z univerzity St.Petersburg. Výsledky z Ruska byly publikovány v Carské akademii vìd a v roce 1872 pro západní Evropu v díle „Les variations de la pesanteur dans les provices occidntales de l'Empire russe". Dalším badatelem, který využil Repsold - Besselova kyvadla, byl J.J.Baeger, øeditel Pruské geodetické spoleènosti. Repsold - Besselova kyvadlo bylo pøijato pro mìøení gravitaèního zrychlení v celé Evropì roku 1874.
Repsold - Besselova kyvadla se používal pro mìøení absolutní gravitace. Stálé kyvadlo s jedním nožovým bøitem se používalo k mìøení relativní gravitace. Stálé kyvadlo používal Bouguer a Karter. Po experimentech s Repsold - Besselovým kyvadlem je Baeger použil pro mìøení gravitaèního zrychlení. Pierce postavil stálé kyvadlo s principy reverzního kyvadla. Prezentoval ho v roce 1880. V období 1881 ÷ 1882 postavil ètyøi stálá reverzní kyvadla, které používala geodetická spoleènost ve Washingtonu. Stálé reverzní kyvadlo popsal jeho asistent E.D. Preston v díle „Determinations of gravity and the magnetic elements in connection with United States scientific expedition to the west coast of Africa 1889 - 90". Pierce dále studoval efekt vizkózního odporu na pohyb Repsold -Besselova kyvadla, pro necylindrické bøity. Defforges vymyslel teorii pro dvì matematická kyvadla stejné hmotnosti, ale s rozdílnou délkou tyèe. Tato teorie eliminovala ohyb závìsu a zakøivení nožových bøitù. Kyvadla dlouhá 1 metr a 0,5 metru postavil podle Defforgesova návrhu firma Brunner Brothers.
Obr. 1.12 Model Besselova kyvadla
Obr. 1.13 Reveryní kyvadlový přístroj podle Defforgse, zkonstruovaný firmou Bruner Brother v Paříži
Maj. Robert von Sternech vyvinul výborný pøístroj pro mìøení relativní gravitace. Jednalo se o reverzní kyvadlo 0,25 metru dlouhé a s dobou kyvu 0,5 sekundy.
Obr. 1.14 Aparát Maj. Sternecka
Kyvadlo mìlo jeden nožový bøit a bylo uloženo do vzduchoprázdné skøínì. Tento pøístroj použil Sternech roku 1887 v Saxonu a v Èechách. Roku 1890 postavil inovovaný pøístroj podle Sternecha Mendenhalla. Mendelhallovo kyvadlo bylo z bronzu, v roce 1920 jej nahradilo kyvadlo z invaru pro jeho nízkou tepelnou roztažnost. Roku 1930 postavil Lt. E.J. Brown vylepšený Mendenhallùv aparát nazvaný Brownùv kyvadlový pøístroj.
Kyvadlo posloužilo také jako pøímí dùkaz Zemì kolem své osy. V roce 1851 v paøížském Pantheonu pøedvedl B.J. Foucault ( 1819 - 1886) kyvadlo s parametry : délka závìsu 67 m, hmotnost 30 kg a doba kmitu 16,4 s. Na tomto kyvadle bylo poprvé pozorováno otáèení Zemì, protože kyvadlo se postupnì samovolnì stáèelo, tak jak se Zemì otáèela viz obr.1.15.
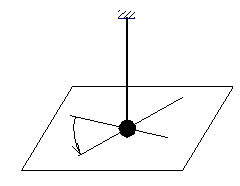
Obr. 1.15 Schéma Foucaltova kyvadla
Toto tvz. Foucaultovo kyvadlo, což je vlastnì matematické kyvadlo s nehmotným závìsem a hmotným bodem na konci kyvadla, bylo v èervenci 1994 postaveno v aule budovy ÈVÚT fakulty strojní a elektrotechnické na Karlovì námìstí ve spolupráci katedry mechaniky strojní fakulty a Planetária Praha.
Jeho parametry jsou :
Pro další hodnoty je nutné znát polohu kyvadla :
Pomocí tohoto kyvadla je možné zjistit tyto hodnoty :
místní tíhové zrychlení g = 9,8040 m·s-2
úhlová rychlost stáèení kyvadla
 |
[1.1.]
|
Kyvadlo je pro lidi tak samozøejmé, že ani nepozorujeme, kde všude v životì jej mùžeme nalézt. Z historie kyvadla jsem vybral dva dùležité obory, kde je vliv kyvadla zøejmý a kyvadlo je zde v jeho klasické podobì. Existuje, ale mnoho lidských oborù, kde kyvadlo ani nehledáme, a pøesto tam je, a tak tomu bude vždy, protože kývající se vìci se vždy budou øídit zákony kyvadla.